Nhờ các liên từ logic, các phán đoán đơn được kết nối với nhau để tạo thành các phán đoán phức. Những liên từ logic này được thể hiện qua các từ nối và giúp kết nối các câu đơn thành các câu phức.
Có nhiều loại liên từ logic khác nhau như:
- Phép hội: được ký hiệu bằng "và", "vừa là... vừa là..."
- Ví dụ: An học giỏi và Bình hát hay.
- Phép tuyển: được ký hiệu bằng "hoặc là", "hay là"
- Ví dụ: Tội tham ô có thể bị phạt tiền hoặc là phạt tù.
- Phép kéo theo: được ký hiệu bằng "nếu... thì..."
- Ví dụ: Nếu trời mưa thì đường bị ướt.
Phán đoán phức là một hàm chân lý, có nghĩa là giá trị chân lý của nó phụ thuộc vào giá trị chân lý của các phán đoán đơn hợp thành. Điều này đặc biệt quan trọng với tính chất của liên từ logic, giúp chúng trở thành hàm chân lý.
Trong logic toán, phán đoán được coi là mệnh đề và các liên từ logic được coi là phép toán mệnh đề (tác tử logic mệnh đề). Để xác định chính xác các tác tử logic mệnh đề, người ta dùng phương pháp cơ bản xác định giá trị chân lý thông qua bảng giá trị chân lý. Ví dụ:
Phép hội:
Có thể biểu diễn bằng bảng giá trị chân lý như sau:
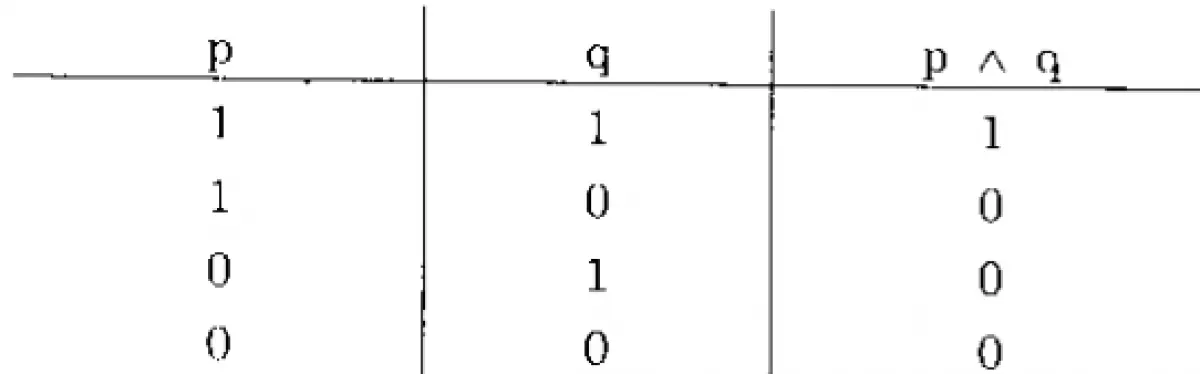
Bảng giá trị chân lý trên chỉ đúng trong phạm vi logic lưỡng trị chân lý. Trong phạm vi đó, mệnh đề phức (hội) chỉ chân thực trong duy nhất một trường hợp, khi cả hai mệnh đề hợp thành đều chân thực. Ví dụ, mệnh đề phức hội: "số 3 là số nhỏ hơn 4 và lớn hơn 2" là chân thực, vì cả hai mệnh đề đơn này hợp thành đều chân thực.
Phép tuyển có hai trường hợp:
- Tuyển lỏng (hay tuyển yếu), ký hiệu là "vee", khi các thành phần hợp thành không loại trừ nhau hoàn toàn. Bảng giá trị chân lý được xác định như sau:

- Tuyển chặt (tuyển mạnh), ký hiệu là "underline vee", khi các thành phần loại trừ nhau hoàn toàn theo luật bài trung. Bảng giá trị chân lý có dạng:

Phép kéo theo:
Bảng giá trị chân lý có dạng:

Phép kéo theo tạo ra phán đoán phức hợp có điều kiện. Điều kiện đó có thể là nguyên nhân gây ra kết quả trong mối liên hệ nhân quả. Ví dụ:
- Nếu trời mưa thì đường bị ướt.
Cũng có thể chỉ là điều kiện hình thức, ví dụ:
- Nếu mực thủy ngân trong nhiệt kế càng dâng lên cao thì trời càng nóng bức.
Điều kiện cần và điều kiện đủ được định nghĩa chính xác bằng tác tử logic kéo theo.
-
Điều kiện đủ: Cứ có p thì chắc chắn có q, suy ra p là điều kiện đủ của q. Ví dụ: Nếu chia hết cho 6 thì đó là số chẵn. Rõ ràng, chia hết cho 6 chỉ là điều kiện đủ chứ không phải là điều kiện cần để là số chẵn, vì các số 2, 4, 8, 10 là số chẵn, nhưng không chia hết cho 6. Ta biểu diễn bằng công thức sau: p → q
-
Điều kiện cần: Nếu không có p thì không thể có q. Ví dụ: Nếu không chia hết cho 6 thì không thể chia hết cho 2. Thực tế, chia hết cho 2 chỉ là điều kiện cần chứ không đủ để chia hết cho 6, vì các số 4, 8, 10, 14 chia hết cho 2, nhưng không chia hết cho 6. Ta biểu diễn bằng công thức sau: (overline p \Rightarrow overline q)
-
Điều kiện cần và đủ: Nếu không có p thì không thể có q và cứ có p thì có q. Ví dụ: Nếu một số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3. Thật vậy, số 36 có tổng các chữ số là 9, 9 chia hết cho 3, đó là thỏa mãn điều kiện đủ. Trường hợp khác, ví dụ như số 34 có tổng các chữ số là 7, 7 không chia hết cho 3, đó là điều kiện cần. Ta biểu diễn bằng công thức sau: (p \Leftrightarrow q)
Các phán đoán phức có hai loại quan hệ chính: so sánh được và không so sánh được. Các phán đoán phức so sánh được với nhau khi có cùng cấu trúc thành phần, nhưng khác nhau về liên từ logic. Ví dụ: (overline {p \wedge q} ) và (overline p \vee \overline q ) và (overline {p \vee q} ) và (overline p \wedge \overline q ,\,\,p \to q) và (overline p \wedge q ,\,\,p \to q) và (overline {p \wedge \overline q } )
Quan hệ so sánh được có hai loại chính: tương thích và không tương thích. Quan hệ tương đương là biểu hiện của tương thích, còn mâu thuẫn, chẳng hạn, là không tương thích.
Ví dụ về quan hệ tương đương lôgic:
Quy tắc De Morgan
- (overline {p \wedge q} = \overline p \vee \overline q )
- (overline {p \vee q} = \overline p \wedge \overline q )
Bằng cách so sánh bảng giá trị chân lý, ta có thể kiểm tra sự đúng đắn của các đẳng thức lôgic trên.
Ví dụ về quan hệ mâu thuẫn Logic: Qua bảng giá trị chân lý nêu trên, ta thấy rõ rằng hai biểu thức (overline {p \wedge q}) và (overline p \vee \overline q ) tương đương lôgic với nhau (vì có giá trị chân lý giống nhau), trong khi hai biểu thức (overline {p \vee q}) và (overline p \wedge \overline q ) không tương đương lôgic với nhau, thậm chí mâu thuẫn loại trừ nhau theo luật bài trung: khi biểu thức này chân thực thì biểu thức kia giả dối và ngược lại.
Như đã biết, các phán đoán đơn có thể so sánh được khi chúng có cùng cấu trúc thành phần, nhưng khác nhau về liên từ logic. Ví dụ, các phán đoán loại A, E, O, I là so sánh được (chúng tương thích hoặc không tương thích với nhau). Trường hợp các phán đoán đơn có chủ từ hay vị từ khác nhau, thì không so sánh được với nhau.
Ví dụ:
- Nguyễn Công Hoan là nhà văn.
- Tô Hoài là nhà văn.
- Ngô Tất Tố là nhà văn.
Không thể so sánh được với nhau vì chúng khác nhau về chủ từ hoặc vị từ hoặc cả chủ từ và vị từ.
Các phán đoán phức cũng có thể không so sánh được với nhau khi các phán đoán đơn hợp thành khác nhau một phần hoặc khác nhau hoàn toàn.
Ví dụ: các phán đoán phức sau không so sánh được với nhau.
- Hà Nội và Bắc Kinh đều là thủ đô: ((S1 \wedge S2) - P1)
- Bắc Kinh và Tokyo đều là những thành phố lớn: ((S2 \wedge S3) - P2)
- Hải Phòng và Đà Nẵng đều là thành phố do Trung ương quản lý: ((S4 \wedge S5) - P3)
Hình thức logic đơn giản nhất của phán đoán đơn có dạng (S - P), trong đó S ký hiệu chủ từ logic, P ký hiệu vị từ logic, dấu trừ ký hiệu hệ từ logic. Còn hình thức logic của phán đoán phức tùy thuộc vào loại liên từ logic, có các dạng thức như: (p \wedge q), (q \vee q), (p \to q), vv...
Logic toán đã tiếp tục hình thức hóa cấu trúc logic của phán đoán, trước hết là của các phán đoán đơn loại A, E, I, O.
Hãy bắt đầu từ các phán đoán đơn cụ thể như:
- Nguyễn Công Hoan là nhà văn.
- Tô Hoài là nhà văn.
- Ngô Tất Tố là nhà văn.
Ta gọi Nguyễn Công Hoan, Tô Hoài, Ngô Tất Tố v.v, là những biến đối tượng, ký hiệu chung là x. Khi đó ta sẽ có hàm phán đoán sau đây: P(x). Hàm phán đoán được biểu đạt thành một câu (một mệnh đề) có chứa biến đối tượng và trở thành phán đoán khi ta thấy biến đối tượng bằng một hằng đối tượng trong một tập hợp xác định các đối tượng. Ở đây có sự tương tự giữa hằng số và biến số trong toán học với hằng đối tượng và biến đối tượng trong lôgic học.
Để hình thức hóa phán đoán chung, dạng như: Mọi kim loại đều dẫn điện và phán đoán riêng như: Một số sinh viên là diễn viên, người ta sử dụng thêm khái niệm lượng từ. Lượng từ là tác tử lôgic định lượng phán đoán. Trường hợp phán đoán chung, đó là lượng từ phổ quát (lượng từ toàn thể), ký hiệu là (forall ), còn trường hợp phán đoán riêng, thì đó là lượng từ tồn tại (lượng từ bộ phận), ký hiệu là (exists ). Khi đó hình thức lôgic của phán oán chung sẽ có dạng ∀xP(x), còn hình thức lôgic của phán doãn riêng sẽ có dạng là (exists )xP(x). Biến đối tượng x trong các dạng phán đoán bị lượng từ hóa như trên gọi là biến liên kết (biến buộc), khác với trường hợp không bị lượng từ hóa thì gọi là biến tự do.
Phép phủ định phán đoán chung và phán đoán riêng sẽ được hình thức hóa theo quy tắc De Morgan như sau:
- (overline forall xP(x) = exists overline {P(x)} )
- (overline exists xP(x) = forall overline {P(x)} )
Vận dụng nguyên tắc hình thức hóa, ta có thể hiểu rõ hơn về hình thức lôgic của các phán đoán loại A, E, O, I.
- Phán đoán loại A:
- (forall x(S(x) \to P(x)) \wedge exists x(S(x) \to P(x)))
- Phán đoán loại E:
- (forall x(S(x) \to \overline {P(x)} ) \wedge exists x(S(x) \to \overline {P(x)} ))
- Phán đoán loại O:
- (exists x(S(x) \to \overline {P(x)} ) \vee forall x(S(x) \to \overline {P(x)} ))
- Phán đoán loại I:
- (exists x(S(x) \to P(x)) \wedge forall x(S(x) \to P(x)))
Nhờ phương pháp hình thức hóa này, người ta đã phát triển lôgic mệnh đề (thực chất là lôgic phán đoán) thành lôgic vị từ (thực chất là lôgic khái niệm). Lôgic mệnh đề và lôgic vị từ là cơ sở của lôgic toán và lôgic ký hiệu tượng trưng.















